Understanding Attention Is All You Need

Introduction

The 2017 paper "Attention Is All You Need" by Vaswani et al. introduced the Transformer architecture, which has since become the foundation for nearly every major advancement in natural language processing. From BERT to GPT-4, understanding Transformers is essential for anyone working in AI/ML.

"The Transformer is the first transduction model relying entirely on self-attention to compute representations of its input and output without using sequence-aligned RNNs or convolution."

- Vaswani et al., 2017

The Problem with RNNs

Before Transformers, recurrent neural networks (RNNs) and their variants (LSTMs, GRUs) dominated sequence modeling tasks. However, they had significant limitations:

• Sequential computation: RNNs process tokens one at a time, making parallelization difficult
• Long-range dependencies: Information gets lost over long sequences despite gating mechanisms
• Training instability: Vanishing and exploding gradients remain challenging

The Attention Mechanism

The core innovation of the Transformer is the self-attention mechanism, which allows the model to weigh the importance of different parts of the input when producing each part of the output.

Scaled Dot-Product Attention

The attention function can be described as mapping a query and a set of key-value pairs to an output:

Where:

• $Q$ (Query): What we're looking for
• $K$ (Key): What we have to match against
• $V$ (Value): The actual information we retrieve
• $d_k$: The dimension of the keys (for scaling)

Multi-Head Attention

Instead of performing a single attention function, the Transformer uses multiple attention heads to capture different types of relationships:

Where each head is computed as:

Implementation in PyTorch

Let's implement the core attention mechanism in PyTorch:

import torch
import torch.nn as nn
import torch.nn.functional as F
import math

class ScaledDotProductAttention(nn.Module):
    """Scaled Dot-Product Attention mechanism."""

    def __init__(self, dropout=0.1):
        super().__init__()
        self.dropout = nn.Dropout(dropout)

    def forward(self, query, key, value, mask=None):
        # query, key, value: (batch, heads, seq_len, d_k)
        d_k = query.size(-1)

        # Compute attention scores
        scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)

        # Apply mask if provided (for decoder self-attention)
        if mask is not None:
            scores = scores.masked_fill(mask == 0, float('-inf'))

        # Softmax and dropout
        attention_weights = F.softmax(scores, dim=-1)
        attention_weights = self.dropout(attention_weights)

        # Apply attention to values
        output = torch.matmul(attention_weights, value)

        return output, attention_weights


class MultiHeadAttention(nn.Module):
    """Multi-Head Attention module."""

    def __init__(self, d_model, num_heads, dropout=0.1):
        super().__init__()
        assert d_model % num_heads == 0

        self.d_model = d_model
        self.num_heads = num_heads
        self.d_k = d_model // num_heads

        # Linear projections
        self.W_q = nn.Linear(d_model, d_model)
        self.W_k = nn.Linear(d_model, d_model)
        self.W_v = nn.Linear(d_model, d_model)
        self.W_o = nn.Linear(d_model, d_model)

        self.attention = ScaledDotProductAttention(dropout)

    def forward(self, query, key, value, mask=None):
        batch_size = query.size(0)

        # Linear projections and reshape for multi-head
        Q = self.W_q(query).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
        K = self.W_k(key).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)
        V = self.W_v(value).view(batch_size, -1, self.num_heads, self.d_k).transpose(1, 2)

        # Apply attention
        attn_output, attn_weights = self.attention(Q, K, V, mask)

        # Concatenate heads and apply final linear
        attn_output = attn_output.transpose(1, 2).contiguous().view(batch_size, -1, self.d_model)
        output = self.W_o(attn_output)

        return output, attn_weights

Positional Encoding

Since attention has no inherent notion of position, the Transformer adds positional encodings to the input embeddings. The original paper uses sinusoidal functions:

class PositionalEncoding(nn.Module):
    """Positional encoding using sinusoidal functions."""

    def __init__(self, d_model, max_len=5000, dropout=0.1):
        super().__init__()
        self.dropout = nn.Dropout(dropout)

        # Create positional encoding matrix
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))

        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)  # (1, max_len, d_model)

        self.register_buffer('pe', pe)

    def forward(self, x):
        # x: (batch, seq_len, d_model)
        x = x + self.pe[:, :x.size(1), :]
        return self.dropout(x)

The Complete Architecture

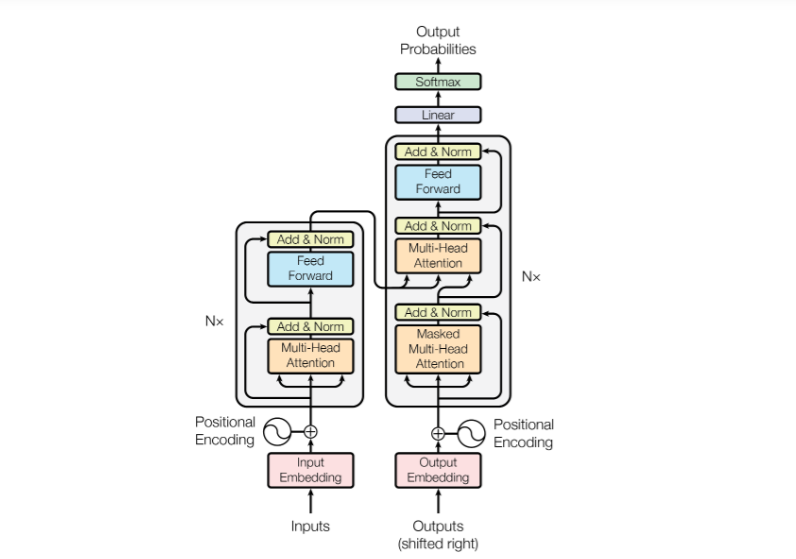
The Transformer consists of an encoder and decoder, each made up of stacked identical layers:

Transformer Architecture Diagram

Encoder Layer

1. Multi-head self-attention
2. Add & Normalize (residual connection + layer norm)
3. Position-wise feed-forward network
4. Add & Normalize

Decoder Layer

1. Masked multi-head self-attention
2. Add & Normalize
3. Multi-head cross-attention (attending to encoder output)
4. Add & Normalize
5. Position-wise feed-forward network
6. Add & Normalize

Why It Matters

The Transformer architecture solved the parallelization problem of RNNs while handling long-range dependencies more effectively. This enabled training on much larger datasets, leading to the foundation models we see today.

Key Takeaways

• Self-attention allows every position to attend to every other position in constant time
• Multi-head attention captures different types of relationships simultaneously
• Positional encodings preserve sequence order information
• Residual connections and layer normalization enable training of deep networks

Further Reading

• Original Paper: Attention Is All You Need
• The Illustrated Transformer by Jay Alammar
• The Annotated Transformer